When we decide to order a diagnostic test, we want to know which test (or tests) will best help us rule-in or rule-out disease in our patient. In the language of clinical epidemiology, we take our initial assessment of the likelihood of disease ("pre-test probability"), do a test to help us shift our suspicion one way or the other, and then determine a final assessment of the likelihood of disease ("post-test probability"). Take a look at the diagram below, which graphically illustrates this process of "revising the probability of disease".
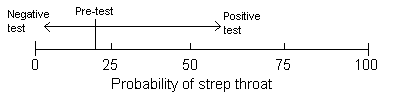
Likelihood ratios tell us how much we should shift our suspicion for a particular test result. Because tests can be positive or negative, there are at least two likelihood ratios for each test. The "positive likelihood ratio" (LR+) tells us how much to increase the probability of disease if the test is positive, while the "negative likelihood ratio" (LR-) tells us how much to decrease it if the test is negative. The formula for calculating the likelihood ratio is:
probability of an individual with the condition having
the test result
LR = probability of an individual without
the condition having the test result
Thus, the positive likelihood ratio is:
probability of an individual with the condition having
a positive test
LR+ = probability of an individual without
the condition having a positive test
Similarly, the negative likelihood ratio is:
probability of an individual with the condition having
a negative test
LR- = probability of an individual without
the condition having a negative test
You can also define the LR+ and LR- in terms of sensitivity and specificity:
LR+ = sensitivity
1-specificityLR- = 1-sensitivity
specificity(Of course, if you're using sensitivity and specificity on a scale of 0 to 100 instead of 0 to 1, the equations would be sensitivity / (100-specificity) and (100-sensitivity)/specificity, respectively).
Let's consider an example:
In a study of the ability of rapid antigen tests to diagnose strep pharyngitis, 90% of patients with strep pharyngitis have a positive rapid antigen test, while only 5% of those without strep pharyngitis have a positive test. The LR+ for the ability of rapid antigen tests to diagnose strep pharyngitis is (select one):
Interpreting likelihood ratios: general guidelines
The first thing to realize about LR's is that an LR > 1 indicates an increased probability that the target disorder is present, and an LR < 1 indicates a decreased probability that the target disorder is present. Correspondingly, an LR = 1 means that the test result does not change the probability of disease at all! The following are general guidelines, which must be correlated with the clinical scenario:
|
LR |
Interpretation |
|
> 10 |
Large and often conclusive increase in the likelihood of disease |
|
5 - 10 |
Moderate increase in the likelihood of disease |
|
2 - 5 |
Small increase in the likelihood of disease |
|
1 - 2 |
Minimal increase in the likelihood of disease |
|
1 |
No change in the likelihood of disease |
|
0.5 - 1.0 |
Minimal decrease in the likelihood of disease |
|
0.2 - 0.5 |
Small decrease in the likelihood of disease |
|
0.1 - 0.2 |
Moderate decrease in the likelihood of disease |
|
< 0.1 |
Large and often conclusive decrease in the likelihood of disease |
The decision to order a test is also based on our initial assessment of the likelihood of the target disorder, and how important it is to rule-in or rule-out disease. For example, a chest x-ray might have a good likelihood ratio for pneumonia. But if you believe a patient has a simple cold, this test, no matter how good the LR, probably shouldn't be ordered. It is sometimes helpful to be able to calculate the exact probability of disease given a positive or negative test. We saw that this is next to impossible using sensitivity and specificity at the bedside (unless you can do Bayes' Theorem in your head!). Next, we'll learn how we can use likelihood ratios to quickly estimate the probability of disease in our patients.